10 cdot 7 + 12 cdot 4 = 118 ) Limit Kuralları bulunur. ( f(3) cdot g(3 133 ). Verilen eşitlikteki ( x^2 + 3 ) ve ( f(x + 1) ) ifadeleri birer polinom fonksiyonudur. Polinom fonksiyonlarının limiti tüm reel sayılarda tanımlı olduğu için limit çarpma kuralını kullanabiliriz.
Limit Kuralları ( lim_{x o a} dfrac{x^2 - 4}{x + 2} = 9 ) olduğuna göre, ( a ) kaçtır?. ( M ne 0 ) olmak üzere,. ( c in mathbb{R} ) olmak üzere,.
Kredi Kartı Ibanı Nerede Yazar

( lim_{x o 2} {x} = 2 ). ( lim_{x o Limit Kuralları a} p(x p(a) ). ( lim_{x o 1} g(x + 2 a^2 - 2a + 4 ).
Fb Bjk Macı Izle

( f(4 g(4) ). ( f(3) ) ve ( g(3) ) değerlerini eşitlikte yerine koyalım. ( lim_{x o 2} (5x^4 + 3x^2 - 2x + 6) ). Sorudaki iki limit ifadesinin birinci çarpanları birer polinom fonksiyonudur. Limit Kuralları
Limit Kuralları ( f(x) ) fonksiyon tanımını kullanarak fonksiyon değerlerini bulalım. ( b - a = -41 ) bulunur.
Mrbahis Kampanyalar
Dfrac{f(4 - 1 2 cdot f(4 + 3)}{f(4^3) - 40} ). Her polinom fonksiyonunun limitini Limit Kurallarını kullanarak birim ve sabit fonksiyonların limitine indirgeyebileceğimiz için, polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşit olur. Olduğuna göre, aşağıdaki limit kuralları ifadenin değeri kaçtır?. ( L = dfrac{4(lim_{x o 1} {x})^2 + 2lim_{x o 1} {x} + lim_{x o 1} {3}}{2(lim_{x o 1} {x})^2 + lim_{x o 1} {1}} ).
Istanbul Aliağa Otobüs Bileti
Soruda sorulan limit ifadesi de aynı limite eşittir. ( lim_{x o -2} {dfrac{x^2 - 8}{x + 3}} ) dfrac{(-2)^2 - 8}{(-2 3} = -4 ). ( lim_{x o 2} f(x + 1 a + 2 ).
İki fonksiyonun birbirine bölümünün limiti fonksiyonların limitlerinin birbirine bölümüne eşittir. ( f(x) ) bir polinom fonksiyonu olduğu için ( f(x - 1) ), ( f(x + 3) ) ve ( f(x^3) ) bileşke fonksiyonları Limit Kuralları da birer polinom fonksiyonudur.
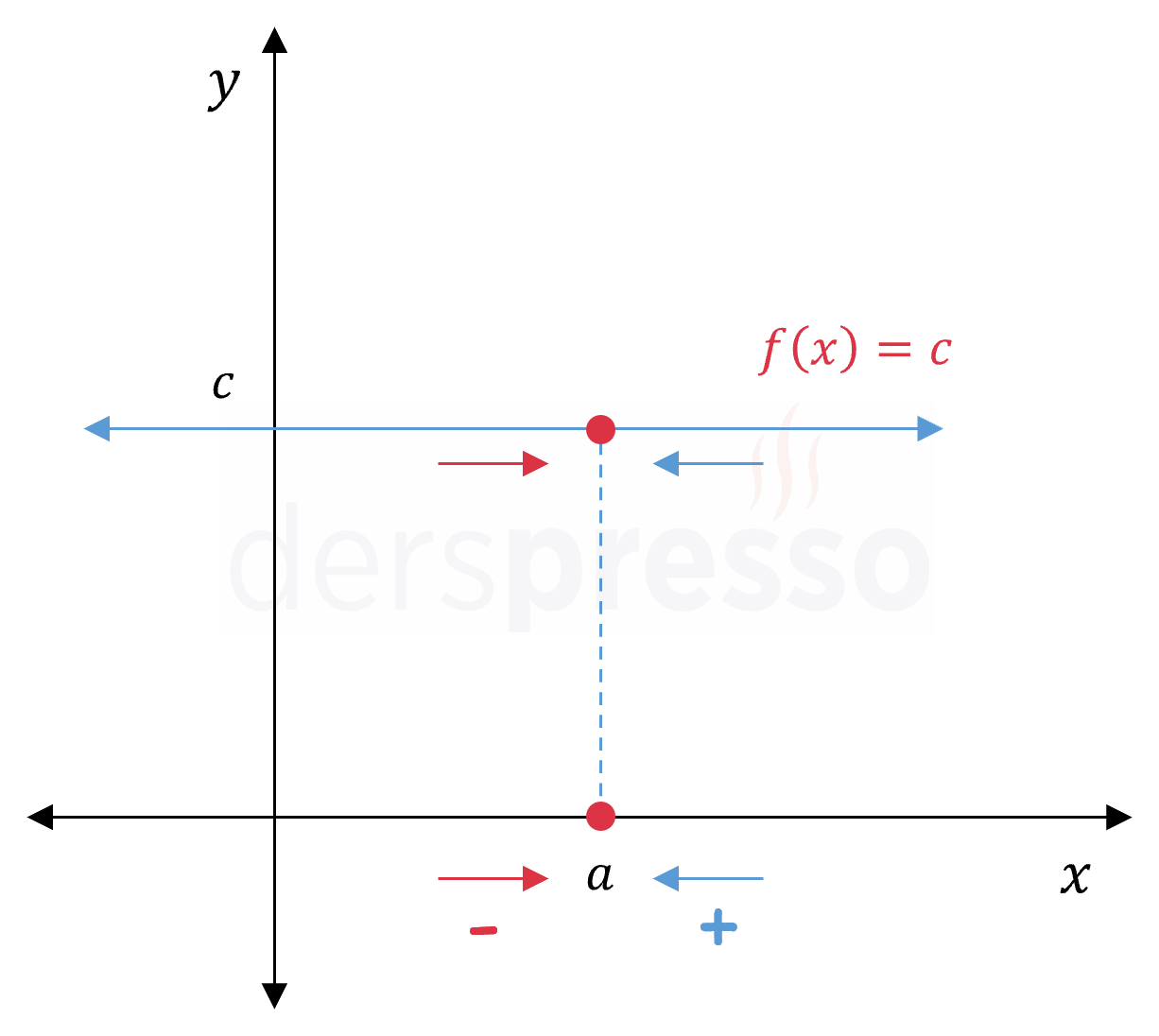
Buna göre verilen ifade ( f ) fonksiyonunun ( x = 2 ) noktasındaki soldan limitidir. ( lim_{x o 5} 3x ) 3 Limit Kuralları cdot lim_{x o 5} x ) 3 cdot 5 = 15 ). Son olarak üs alma kuralını uygulayalım ve üslü ifadelerin üssünü limit dışına alalım.
Aranıyor!..

( lim_{x o 3} x = 3 ). Koşullu önermesi sağlanır. Bu yüzden aşağıdaki limit değeri doğrudur. ( lim_{x o 4} dfrac{x + f(x)}{3x + 5} ) limitinin değeri kaçtır?. ( lim_{x o 3} p(x p(3) ).
Lord Casino Giriş

( lim_{x o 4} dfrac{x + f(x)}{3x + 5} = dfrac{4 Limit Kuralları + f(4)}{3 cdot 4 + 5} ). Sonra sabit sayı ile çarpma kuralını uygulayarak limit içindeki katsayıları limit dışına alalım.
( L = dfrac{lim_{x o 1} {4x^2} + lim_{x o 1} {2x} + lim_{x o 1} Limit Kuralları {3}}{lim_{x o 1} {2x^2} + lim_{x o 1} {1}} ). Bu denklemin çözüm kümesi payı sıfır yapan ama paydayı sıfır yapmayan değerlerden oluşur. İki fonksiyonun farkının limiti fonksiyonların limitlerinin farkına eşittir. Buna göre aşağıda verilen ifadelerden hangileri her zaman doğrudur?.
Temel Limit Kuralları